DEFINICIÓN DE LAS DERIVADAS

UNA DERIVADA ES UNA FUNCIÓN ES UNA RAPIDEZ QUE CON LA CUAL CAMBIA EL VALOR DE UNA FUNCIÓN TAMBIÉN CAMBIARA EL VALOR DE LA VARIABLE, CALCULA CON LA BREVEDAD EL LIMITE DE UNA FUNCIÓN SIENDO INTERVALO .
TAMBIÉN PUEDE SER EL RESULTADO DE UNA  RECTA DE UNA FUNCIÓN EN UN PUNTO CUALQUIERA Y EN ESE PUNTO DE ESA FUNCIÓN PUEDE INTERPRETARSE GEOMÉTRICA MENTE YA QUE CORRESPONDE A UNA PENDIENTE DE LA RECTA DE DICHA FUNCIÓN EN UN PUNTO DICHO

http://www.youtube.com/watch?v=k8w8P03VqNA&feature=fvst

cabri

Triangulo Rectangulo

Grandes Físico, Filósofos y Matemáticos

                                             NEWTON
 

Primera Ley o Ley de Inercia

Todo cuerpo permanece en su estado de reposo o de movimiento rectilíneo uniforme a menos que otros cuerpos actúen sobre él.

Segunda Ley o Principio Fundamental de la Dinámica

La fuerza que actua sobre un cuerpo es directamente proporcional a su aceleración

Tercera Ley o Principio de acción-reacción

Cuando un cuerpo ejerce una fuerza sobre otro, éste ejerce sobre el primero una fuerza igual y de sentido opuesto.

GALILEO GALILEI 

 (1564 - 1642) “ El universo está escrito en lenguaje matemático” Para Galileo, todo fenómeno natural puede explicarse matemáticamente . 

PITAGORAS

 fue un filósofo y matemático griego, considerado el primer matemático puro. Contribuyó de manera significativa en el avance de la matemática helénica, la geometría y la aritmética derivada particularmente de las relaciones numéricas, aplicadas por ejemplo a la teoría de pesos y medidas, a la teoría de la música o la astronomía. Es el fundador de la hermandad pitagórica, una sociedad que, si bien era de naturaleza predominantemente religiosa, se interesaba también en medicina, cosmología, filosofía, ética y política, entre otras disciplinas; el pitagorismo formuló principios que influenciaron a tanto a Platón como a Aristóteles, y de manera más general, al posterior desarrollo de la matemática y la filosofía racional en Occidente.

Historia De La Geometria

Definición de Geometría

matemática que se ocupa del estudio de las propiedades de las figuras geométricas en el plano o el espacio, como son: puntos, rectas, planos, politopos (incluyendo paralelas, perpendiculares, curvas, superficies, polígonos, poliedros...)
Es la base teórica de la geometría descriptiva o del dibujo técnico. También da fundamento a instrumentos como el compás, el teodolito, el pantógrafo o el sistema de posicionamiento global (en especial cuando se la considera en combinación con el análisis matemático y sobre todo con las ecuaciones diferenciales).

Angulos y Clases de Angulos

ANGULOS

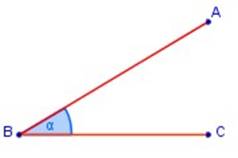
        Es la figura formada por 2 semirectas que parten de un mismo punto. Las semirectas se llaman lados y el punto común vértice. 

 Clases de Angulos


Un ángulo es una figura geométrica formada en una superficie por dos líneas que parten de un mismo punto.
También podemos decir que un ángulo es la abertura formada por dos rayos llamados lados, que tienen un origen común llamado vértice.

El ángulo se anota: 


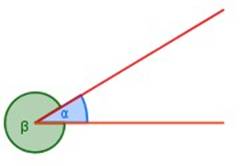
Dos rectas con un origen común determinan siempre dos porciones del plano y por tanto dos ángulos, α y β.
Al ángulo α se le llama ángulo convexo, mientras que el ángulo β es cóncavo.

Los ángulos pueden clasificarse según su medida en cinco tipos:

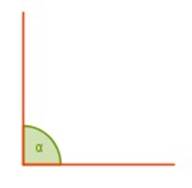
Ángulo recto: es aquel cuya medida es de 90°

∠ α = 90°

Ángulo agudo: es aquel cuya medida es menor que 90°

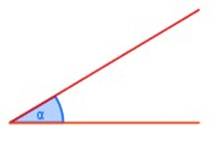
∠ α = < 90°

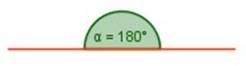
Ángulo extendido: es aquel cuya medida es de 180°

∠ α = 180°

Ángulo obtuso: es aquel cuya medida es mayor que 90° y menor que 180°

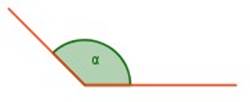
∠ α = > 90° < 180º

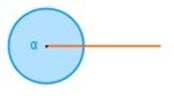
Ángulo completo: es aquel cuya medida es de 360°

∠ α = 360°